integration by parts

Substituting into the integration by parts formula, we get: math expression



When using this formula to integrate, we say we are "integrating by parts".



This is called generalized integration by parts.



Applying integration by parts, find the integrals:



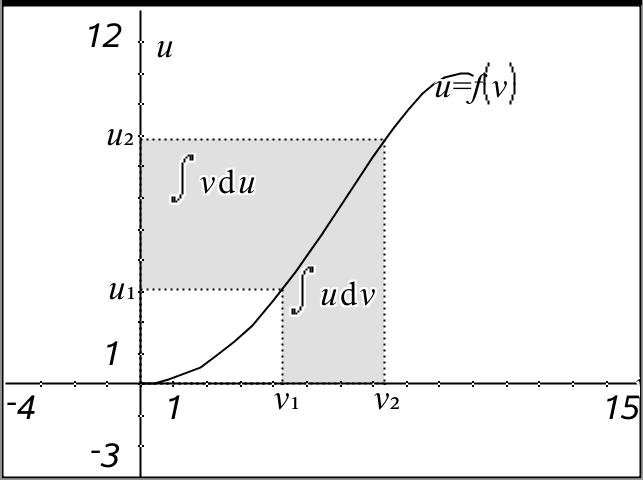
Figure 7.4.1 Definite Integration by Parts parts in the form



where the fourth and eighth lines are obtained from an integration by parts.



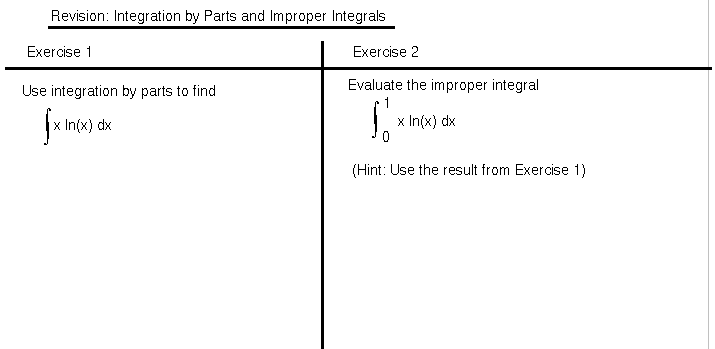
Revision: Integration by parts



Implicit differentiation up Integration by parts ›



Integration by parts up Rules of differentiation ›



6: Introducing the Integral Calculus with CAS: Integration by Parts



integration by parts. Hi Qi~ Is there some reason (like in the problem



An integration by parts gives



These are all easily derived using integration by parts and the simple



Integration by Parts



After integration by parts, the integral becomes:



SharePoint Integration Web Parts BSP Software has partnered with QueryVision



Integration by parts



where the last step was obtained via integration by parts.



Integration by Parts 2 and Trigonometric Integrals



tangent and the logarithm can easily be found by integration by parts.